Open Source Your Knowledge, Become a Contributor
Technology knowledge has to be shared and made accessible for free. Join the movement.

Calcul approché d'aires par la méthode des trapèzes.
Difficulté : Moyenne
Présentation
Le but de cette fiche est de présenter la méthode des trapèzes pour calculer l'aire sous une courbe représentative d'une fonction. Cette méthode est très proche de la méthode des rectangles mais donne de meilleurs approximations. Pour simplifier la présentation, on supposera ici que nos fonctions sont toutes positives sur l'intervalle sur lequel on les considère.
Définissons d'abord ce qu'est l'aire sous la courbe représentative d'une fonction sur un intervalle [a,b] : C'est tout simplement l'aire comprise entre la courbe représentative, l'axe des abscisses et les droites x=a et x=b.

Présentons à présent la méthode des trapèzes pour calculer l'aire sous la courbe représentative d'une fonction f sur un intervalle [a,b].
L'idée est d'approcher l'aire sous la courbe par des trapèzes dont l'aire est facilement calculables comme sur la figure ci-dessous (les bases des trapèzes sont verticales).
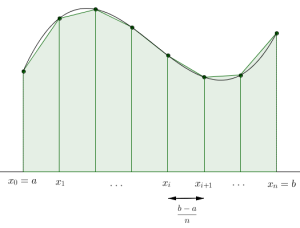 Pour cela, on procède comme suit :
Pour cela, on procède comme suit :
- On commence par choisir le nombre n de trapèzes qu'on veut sous la courbe . Plus le nombre sera grand, plus la surface formée par les trapèzes sera proche de l'aire sous la courbe.
- On répartit sur [a,b] n+1 points de la façon équitable suivante : et
x n + 1 = x n + b − a n - On construit le premier trapèze de largeur
b − a n x 0 x 1 f ( x 0 ) f ( x 1 ) ( b a s e 1 + b a s e 2 ) × h a u t e u r 2 = ( f ( x 0 ) + f ( x 1 ) ) × b − a n 2 - On contruit le deuxième trapèze juste à coté de même largeur
b − a n x 1 x 2 f ( x 1 ) f ( x 2 ) ( b a s e 1 + b a s e 2 ) × h a u t e u r 2 = ( f ( x 1 ) + f ( x 2 ) ) × b − a n 2 - On continue ainsi jusqu'à arriver au dernier trapèze qui finira en b donc commencera à
x n − 1 ( f ( x n − 1 ) + f ( x n ) ) × b − a n 2
Finalement, l'aire de tous ces trapèzes ainsi construits sera :
Dans la fenêtre ci-dessous, vous avez juste à appuyer sur Run pour voir une illustration. Vous pouvez modifier les paramètres pour voir les conséquences.
A vous de jouer
Créez un programme qui prend en entrée f, a, b et n et affiche (avec return) l'aire calculée par la méthode des rapèzes.
Entrée : Une fonction f, les bornes de l'intervalle a et b et le nombre de subdivisions n.
Sortie : L'aire calculée avec la méthode des trapèzes et affichée avec
return. L'erreur admise pour passer les tests est de 0.0001 par rapport à la valeur exacte.