Descente de gradient (fonction de deux variables)

guillitte

12K views

GitHub

Open Source Your Knowledge, Become a Contributor

Technology knowledge has to be shared and made accessible for free. Join the movement.

Create Content

Bonjour!

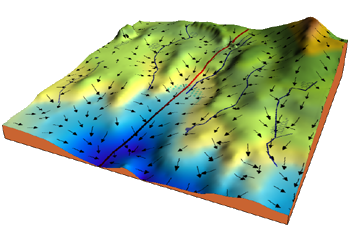
Gradient descent

Ce programme python illustre l'algorithme de descente de gradient pour rechercher un minimum local d'une fonction f de deux variables réelles.
Son principe est simple : pour trouver le minimum, il suffit d'effectuer des petits pas dans le sens de la descente, juqu'au momment où la pente s'annule.
Nous rechercherons un minimum de la fonction f telle que f(x,y) = (x-2)²+(y-3)². On peut aisément deviner ce minimum car f(x,y) est une somme de carrés.
Pour une fonction de deux variables, le gradient est un vecteur dont les composantes sont les dérivées partielles :

df/dx = 2(x-2)
df/dy = 2(y-3)

Sa direction donne la ligne de pente et sa norme donne l'inclinaison.

Ce programme comporte deux versions de l'algorithme :

La première utilise le gradient analytique de f, qui doit lui être fournie.
La seconde utilise une approximation numérique de ce gradient.

import math 
def f(x, y):
    return (x-2)**2+(y-3)**2
def df(x, y):
    return 2*(x-2) , 2*(y-3) #composantes du gradient : df/dx , df/dy
def descente1(f, df, x, y, alpha=1e-2, eps=1e-6, maxIter=1000):
    # Recherche le minimum d'une fonction f par descente de gradient
    # df doit être la dérivée de f
    # x,y sont les valeurs initiales
    # alpha est le taux d'apprentissage qui détermine la rapidité de la descente (par défaut 1/100)
    # eps est la précision souhaitée (par défaut 1/1000000)
    # maxIter est le nombre maximum d'itération (par défaut 1000)
    
    gradx, grady = df(x,y)
    grad = math.sqrt(gradx**2+grady**2) # norme du gradient (math.sqrt est la racine carrée)
    i=0
    while abs(grad)>eps: # tant que la pente n'est pas approximativement nulle
        gradx, grady = df(x,y) # on calcule la pente
        grad = math.sqrt(gradx**2+grady**2) # norme du gradient
        x = x-alpha*gradx # on effectue un petit pas vers le bas selon x
        y = y-alpha*grady # on effectue un petit pas vers le bas selon y
        i += 1
        #print(i, x, y , gradx, grady) # décommenter cette ligne pour imprimer les itérations
        if i > maxIter:
            return None # on abandonne si le nombre d'itérations est trop élevé
    return x,y
def descente2(f, x, y, alpha=1e-2, eps=1e-6, maxIter=1000):
    # Recherche le minimum d'une fonction f par descente de gradient avec dérivée numérique
    # x,y sont les valeurs initiales
    # alpha est le taux d'apprentissage qui détermine la rapidité de la descente (par défaut 1/100)
    # eps est la précision souhaitée (par défaut 1/1000000)
    # maxIter est le nombre maximum d'itération (par défaut 1000)    
    
    grad = 1
    i=0
    while abs(grad)>eps:
        gradx = (f(x+eps,y)-f(x-eps,y))/(2*eps) #approximation numérique de la dérivée df/dx
        grady = (f(x, y+eps)-f(x, y-eps))/(2*eps) #approximation numérique de la dérivée df/dy
        grad = math.sqrt(gradx**2+grady**2) # norme du gradient
        x = x-alpha*gradx # on effectue un petit pas vers le bas selon x
        y = y-alpha*grady # on effectue un petit pas vers le bas selon y
        i += 1
        #print(i, x, y, gradx, grady) # décommenter cette ligne pour imprimer les itérations
        if i > maxIter:
            return None # on abandonne si le nombre d'itérations est trop élevé

Exercice

Déterminer unn minimum local de la fonction f définie par f(x,y) = x² + 2 y² - xy + 5x - 4y - 5

Open Source Your Knowledge: become a Contributor and help others learn. Create New Content

Open Source Your Knowledge, Become a Contributor

Bonjour!

Exercice

Descente de gradient

Méthode d'Archimede

PYTHON: BEGINNER QUIZ (10 Questions)

PYTHON STRING METHODS: center(), rjust() and ljust().